https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
문제
- 45656이란 수를 보자. 이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
- N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 단, 0으로 시작하는 수는 계단수가 아니다.
- 첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
아이디어
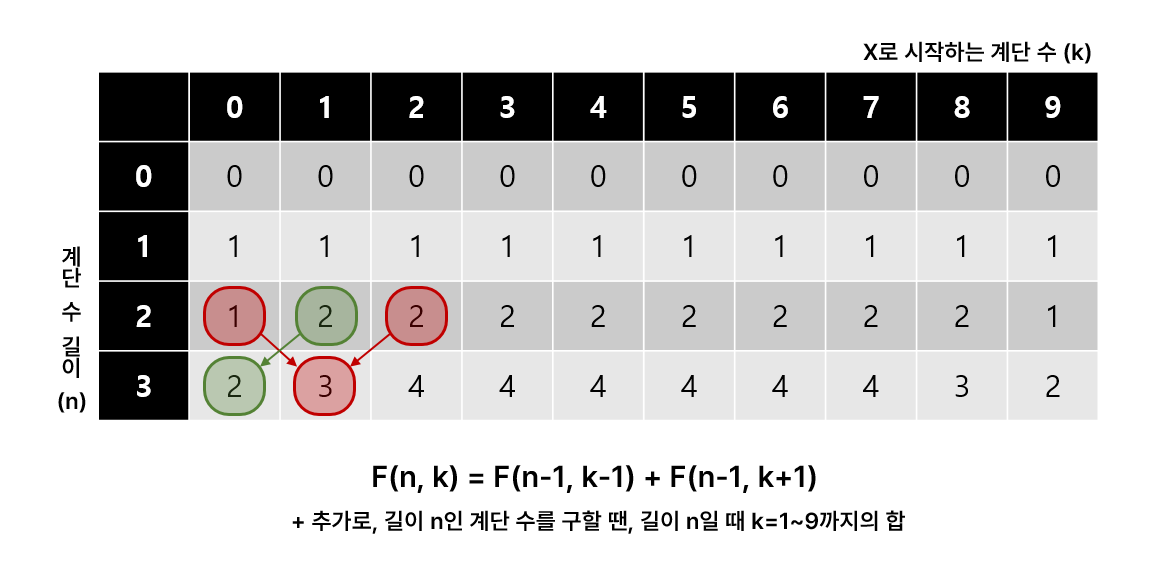
먼저 결론부터 말하자면 다음과 같다. F(n, k) = F(n-1, k-1) + F(n-1, k+1) 이라는 점화식으로 2차원 배열을 채운 후, 길이 n인 계단 수를 구할 때는 길이 n일 때 k=1~9까지의 합을 구하면 된다.
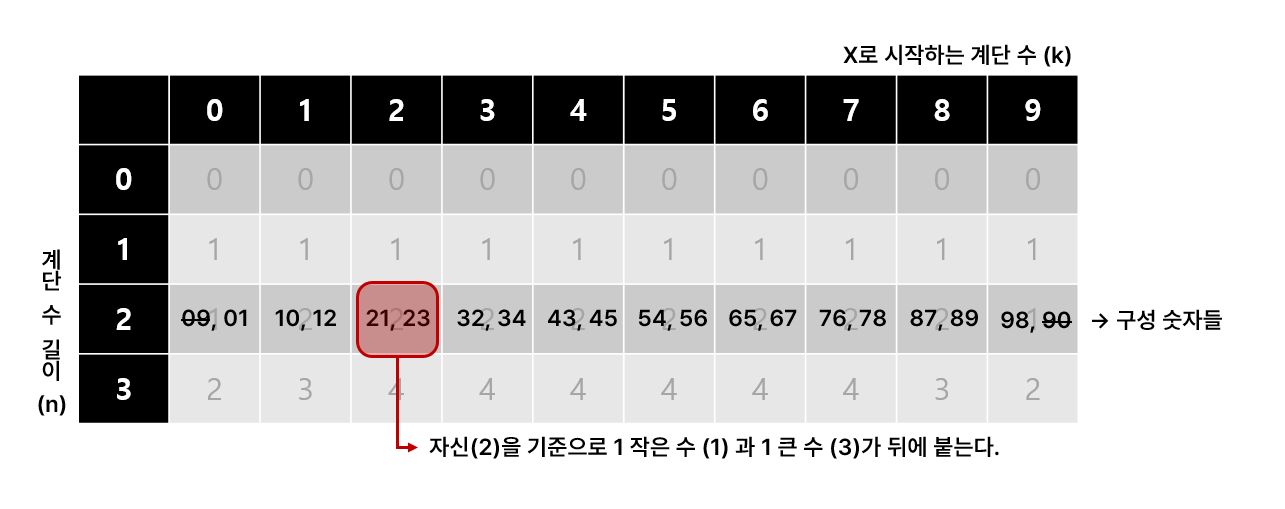
그러면 점화식 결론이 어떻게 나왔는지 생각해보자.
규칙성을 찾기 위해 n이 2, 3일 때 정도는 직접 작성해보는 것이 좋다. n이 2일 때 각 자리의 구성 요소들은 위 표와 같다.
자신을 기준으로 1작은 수와 1큰 수를 붙여서 계단 수를 만들 수 있는 것을 알 수 있다.
이 때, 표의 맨 앞인 0은 1 작은 수 (09)와 1 큰 수 (01) 로 구성되는데, 09는 계단 수가 아니므로 제외한다.
표의 맨 끝인 9 역시 90이 계단 수가 아니므로 제외한다.

n=3일 때도 작성해보자. 많이 작성할 필요도 없다.
k=2일 때(2로 시작하는 계단 수)를 작성하려고 보면, 2 다음에는 1이나 3이 올 수 있으니 21☆과 23☆이 될 수 있다.
그럼 ☆은 어떻게 정해지는가? ☆을 정하기 위해서는 10의 자리수만 보면 된다. 그 값은 n=2일 때 k=1, 3 값과 같다.
마지막으로 답을 낼 때는 1~9로 시작하는 계단 수를 모두 더해서 내면 된다. 0으로 시작하는 값은 계단 수가 아니다.
전체 코드
N = int(input())
DP = [[0] * 10 for _ in range(N+1)]
# x축: 0__, 1__, 2__ ... => x로 시작하는 계단 수
# y축: 숫자 길이
for i in range(10):
DP[1][i] = 1
for r in range(2, N+1):
for c in range(10):
tmp1 = (c-1 >= 0) and DP[r-1][c-1]
tmp2 = (c+1 < 10) and DP[r-1][c+1]
# 11시, 1시 방향에 위치한 두 값을 더해준다.
DP[r][c] = (tmp1 + tmp2) % 1000000000
# DP[N][0]은 0으로 시작하는 계단 수는 불가능하므로 빼준다
# 합했을 때 % 연산을 안 해서 틀렸었다.
print(sum(DP[N][1:]) % 1000000000)
다른 사람 코드
N = int(input())
DP = [[0]*10 for i in range(101)]
DP[1] = [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
for i in range(2, N+1):
for j in range(10):
if j == 0:
DP[i][j] = DP[i-1][j+1]
elif j == 9:
DP[i][j] = DP[i-1][j-1]
else:
DP[i][j] = DP[i-1][j+1] + DP[i-1][j-1]
result = 0
for i in range(0, 10):
result += DP[N][i]
print(result % 1000000000)
나는 x축의 값을 가장 큰 자리 수 값으로 잡았는데, 이 사람의 경우 가장 작은 자리 수 값으로 잡았다.
나는 가장 큰 자리수 값이 0일 때 계단수가 아니기 때문에 result에서 인덱스 0의 값은 제외해줬는데, 이 사람의 경우 가장 작은 자리수 값이 0일 때도 계단수가 될 수 있기 때문에 인덱스 0의 값도 포함시켜준다.
'APS > BOJ' 카테고리의 다른 글
| [Python / BOJ 13459] 구슬 탈출 (0) | 2022.03.03 |
|---|---|
| [Python / BOJ 18808] 스티커 붙이기 (0) | 2022.03.03 |
| [Python / BOJ 12865] 평범한 배낭 (0) | 2022.01.24 |
| [Python / BOJ 3151] 합이 0 (0) | 2022.01.17 |
| [Python / BOJ 23290] 마법사 상어와 복제 (0) | 2021.12.14 |