https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
문제
- N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가진다.
- 최대 K만큼의 무게를 배낭에 넣을 수 있다. 넣을 수 있는 물건들의 가치 최대값은 얼마인가?
[BOJ 12865] 평범한 배낭은 기본적인 0-1 배낭 문제이다.

배낭 문제는 담을 수 있는 무게의 최댓값이 정해져 있고 일정 가치와 무게가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제를 말한다.
배낭문제는 짐을 쪼갤 수 있는 경우(무게가 소수일 수 있는 경우)와 짐을 쪼갤 수 없는 경우(이 경우 짐의 무게는 0 이상의 정수만 가능) 두 가지로 나눌 수 있는데, 짐을 쪼갤 수 있는 경우의 배낭문제를 분할가능 배낭문제(Fractional Knapsack Problem), 짐을 쪼갤 수 없는 경우의 배낭문제를 0-1 배낭문제(0-1 Knapsack Problem)라 부른다.
풀이
동적 계획법 (DP) 는 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법이다. 이 문제 역시 간단한 작은 문제로 나누어 풀 수 있다. 하지만 아래와 같이 실수를 할 수 있으니 조심할 것. 해당 내용들은 이 곳 / 코딩테스트, 중급, knapsack problem 내용을 정리한 것이다.
a. 잘못된 방법

b. 올바른 방법
b-1. bottom-up 방식
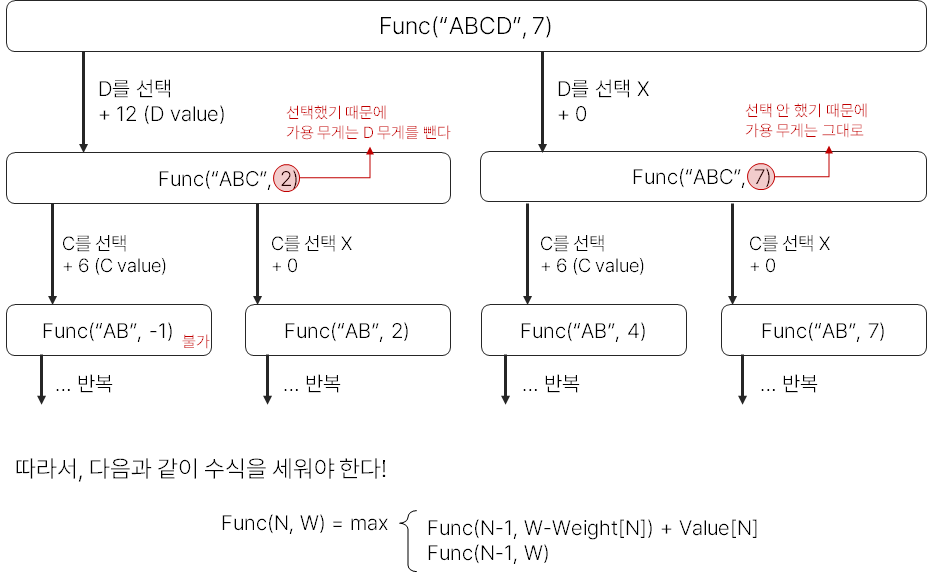
수식을 세우고 문제로 돌아오면 우리가 구해야 하는 값이 Func(4, 7)이라는 것을 알 수 있다.
2차원 dp배열을 만들어 위치를 찾으면 다음 그림과 같다.

빨간 동그라미인 Func(4, 7)은 Func(3, 2) + 12와 Func(3, 7) 중 큰 값을 선택하면 된다.
또, 초록 동그라미 Func(3, 2)와 Func(3, 7)을 구하기 위해서는 수식을 반복하면 된다.
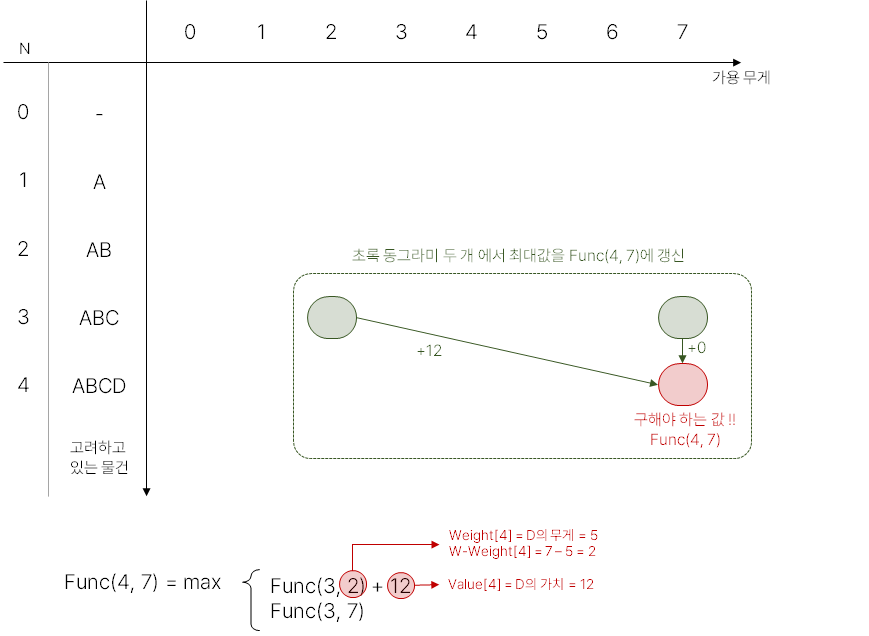
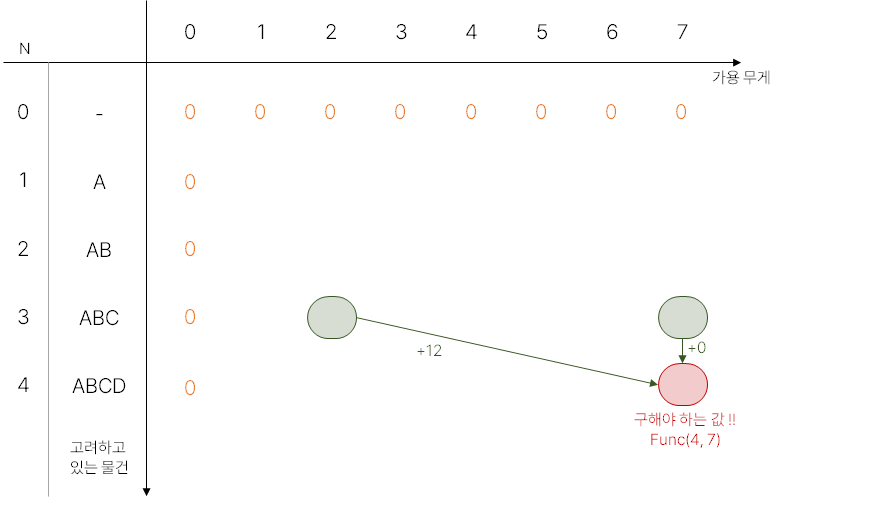
수식을 반복하다보면 표의 첫 행, 첫 열로 돌아온다.
해당 부분들은 가용 무게가 0이거나, 고려하고 있는 물건이 없으므로 값이 모두 0이게 된다.
b-2. top-down 방식
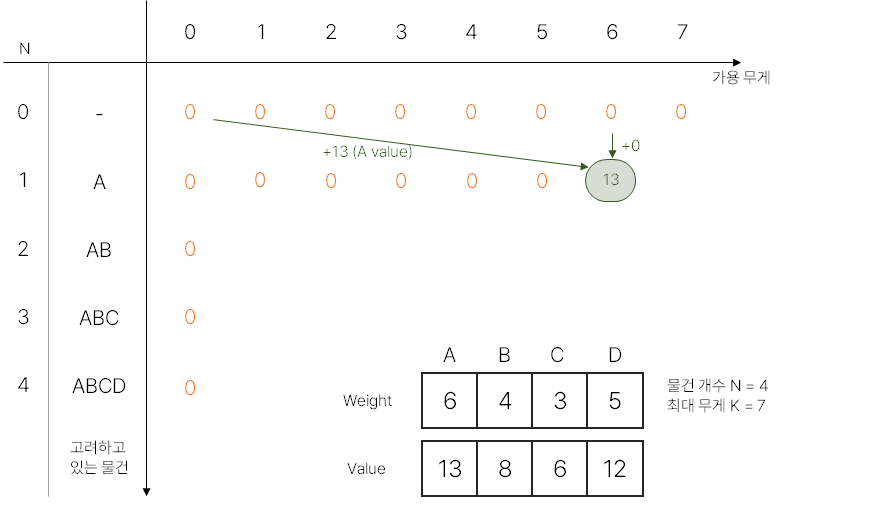
이 경우, 가용 무게가 넉넉하여 물건을 선택할 수 있을 경우 왼쪽에서 화살표가 오고, 물건을 선택할 수 없을 경우 바로 위에서 화살표가 온다. 두 화살표의 최대값으로 갱신하면 된다.

실제 문제에선, A를 처음 선택할 수 있는 경우가 무게 6일 때 이므로 초록 부분에 13이 처음 갱신된다.
코드
# b-2. top-down 방식
N, K = map(int, input().split())
# (1, 1) 부터 시작하기 위해 [0, 0] 삽입
IN = [[0, 0]]
for _ in range(N):
IN.append(list(map(int, input().split())))
dp = [[0 for _ in range(K + 1)] for _ in range(N + 1)]
for i in range(1, N + 1):
for j in range(1, K + 1):
weight = IN[i][0]
value = IN[i][1]
# weight(선택한 물건의 무게) 보다 j(가용 무게)가 작으면 위의 값을 그대로 가져온다
if j < weight:
dp[i][j] = dp[i - 1][j]
# weight 보다 j가 크면 화살표는 왼쪽에서도 올 수 있으니, 큰 값으로 갱신한다.
# 왼쪽 화살표 => 이전 행 & 가용무게 - 선택 물건 무게 & 가치 더하기 => dp[i-1][j-weight] + value
else:
dp[i][j] = max(dp[i - 1][j - weight] + value, dp[i - 1][j])
print(dp[N][K])
다른 사람 코드
N, K = map(int, input().split())
ary = [list(map(int, input().split())) for _ in range(N)]
dp = [0] * (K+1)
for weight, val in ary:
for j in range(K, weight-1, -1):
dp[j] = max(dp[j], dp[j-weight] + val)
print(dp[K])
'APS > BOJ' 카테고리의 다른 글
| [Python / BOJ 18808] 스티커 붙이기 (0) | 2022.03.03 |
|---|---|
| [Python / BOJ 10844] 쉬운 계단 수 (0) | 2022.02.22 |
| [Python / BOJ 3151] 합이 0 (0) | 2022.01.17 |
| [Python / BOJ 23290] 마법사 상어와 복제 (0) | 2021.12.14 |
| [Python / BOJ 23291] 어항 정리 (0) | 2021.12.14 |